底面积怎么求？一文搞懂各类几何体的计算方法与常见误区

在学习几何的过程中，我们经常会遇到“底面积怎么求”这个问题。很多人一开始会觉得它只是个简单的计算步骤，但其实底面积是连接平面图形与立体图形的重要桥梁。它是理解和计算体积、表面积的基础，贯穿于数学、物理乃至工程应用之中。理解底面积的本质，不仅能帮助我们更准确地解题，还能提升对空间结构的整体感知。

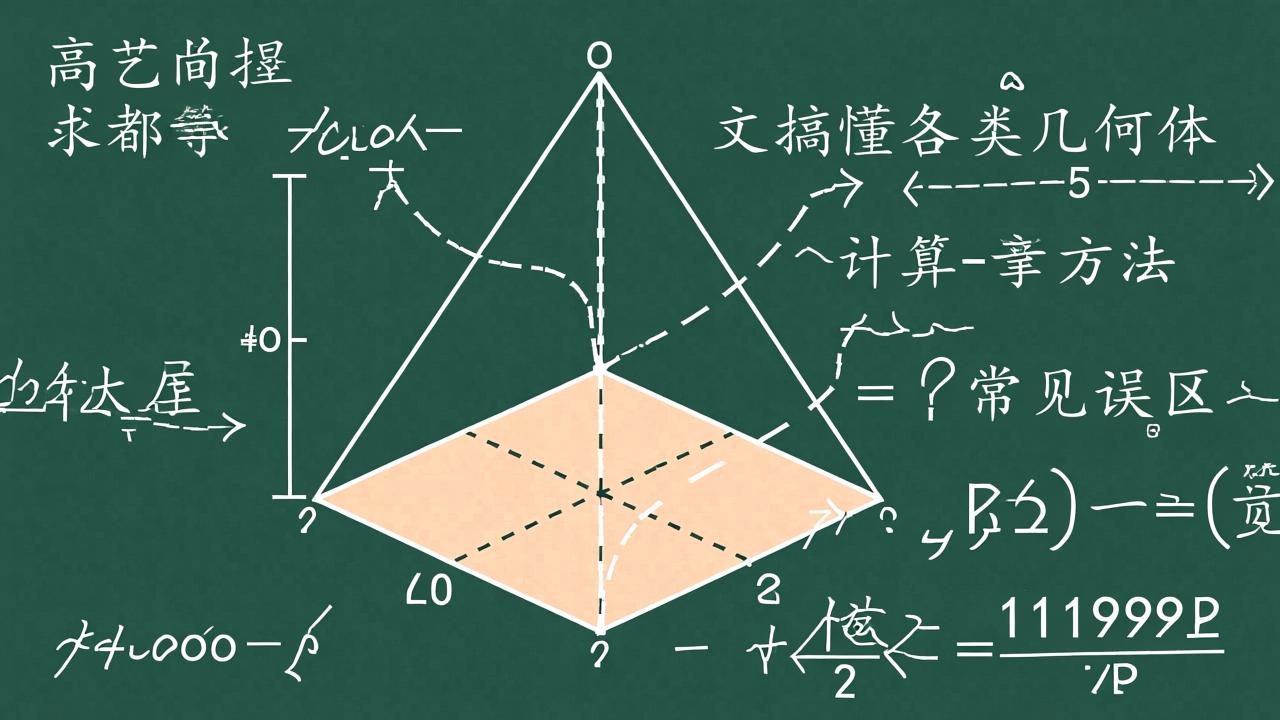
底面积这个概念听起来简单，但它背后藏着不少值得深挖的内容。从最常见的长方体到复杂的棱柱体，每一个立体图形都有它的“底”。而这个“底”并不总是位于最下面的那一面，这一点常常让人误解。接下来我会带你一步步拆解什么是底面积，它为什么重要，以及不同形状的底面是如何分类和识别的。

1.1 什么是底面积：定义与几何意义

底面积，顾名思义，就是某个立体图形底部那个面的面积。但在数学中，“底”不一定非得是放在桌面上的那一面。比如一个竖立的圆柱，它的底面是上下两个圆形之一；但如果我把这个圆柱横过来放，虽然接触地面的是侧面，可数学上我们仍然认为原来的圆形才是它的底面。所以说，底面更多是由图形结构决定的，而不是由摆放方式决定的。

我刚开始学的时候也以为底面就是“最下面”的那个面，结果做题时总是出错。后来我才明白，底面积其实是用来作为计算基准的那个面。比如在算体积时，我们会用“底面积×高”，这里的底面积就是一个参考面，通常是图形中一对平行且全等的面中的一个。像棱柱、圆柱这些图形，上下底面是一样的，选哪一个都行。这种设定让公式更加统一，也方便记忆和应用。

1.2 底面积在体积与表面积计算中的作用

说到体积，你有没有想过为什么大多数体积公式都是“底面积×高”？这可不是巧合。想象一下盖房子，一层层往上垒砖块，每一层的大小就是底面积，垒了多少层就是高。所以总体积自然就是每层面积乘以层数。这个思路适用于很多规则立体图形，比如长方体、圆柱、棱柱等等。

我在辅导学生时常用一个比喻：底面积就像是蛋糕的每一层，高度就是层数。你想知道整个蛋糕有多大，就得先知道每层有多大。同样的道理，就算表面积也需要先搞清楚底面积。比如一个长方体的表面积是六个面加起来，其中有两个是底面，另外四个是侧面。如果你连底面积都不会算，那总表面积肯定也会出问题。

而且很多实际问题，比如水箱能装多少水、房间要刷多大面积的墙，都需要先确定底面积。可以说，掌握了底面积，就等于拿到了打开立体几何大门的一把钥匙。

1.3 常见几何体的底面形状分类

不同的立体图形，它们的底面形状也不一样。最常见的有长方形、正方形、三角形和圆形。比如长方体的底面是个长方形，正方体的底面是正方形，三棱柱的底面是三角形，而圆柱和圆锥的底面则是圆形。这些基本形状决定了我们该用哪个面积公式来计算。

有时候我会让学生画图辅助理解。比如看到一个金字塔形状的帐篷，他们第一反应可能是“这是三角形”，但其实它的底面很可能是正方形或矩形。这时候就要提醒自己：别被外形迷惑，要看哪个面是用来支撑整体结构的，或者哪两个面是平行且相同的。对于像圆锥这样的图形，虽然只有一个底面（另一个顶点），但我们依然把它那个圆形当作底。

我还发现，有些同学容易把斜放的图形搞混。比如一个斜着放的三棱柱，看起来像是侧面朝下，但其实只要找到那两个互相平行且一样的三角形面，其中一个就是底面。认清这一点，底面积怎么求的问题就迎刃而解了。

现在我们已经明白了底面积到底是什么，也知道它在几何计算中的重要性。接下来最实际的问题来了：面对不同的立体图形，我们到底该怎么求它们的底面积？每种图形都有自己的特点，对应的底面积计算方法也不一样。今天我就带你一个一个来看，从最常见的圆柱开始，再到长方体、正方体，还有棱柱和圆锥这些稍微复杂一点的图形。

2.1 圆柱体底面积怎么求：公式推导与实例解析

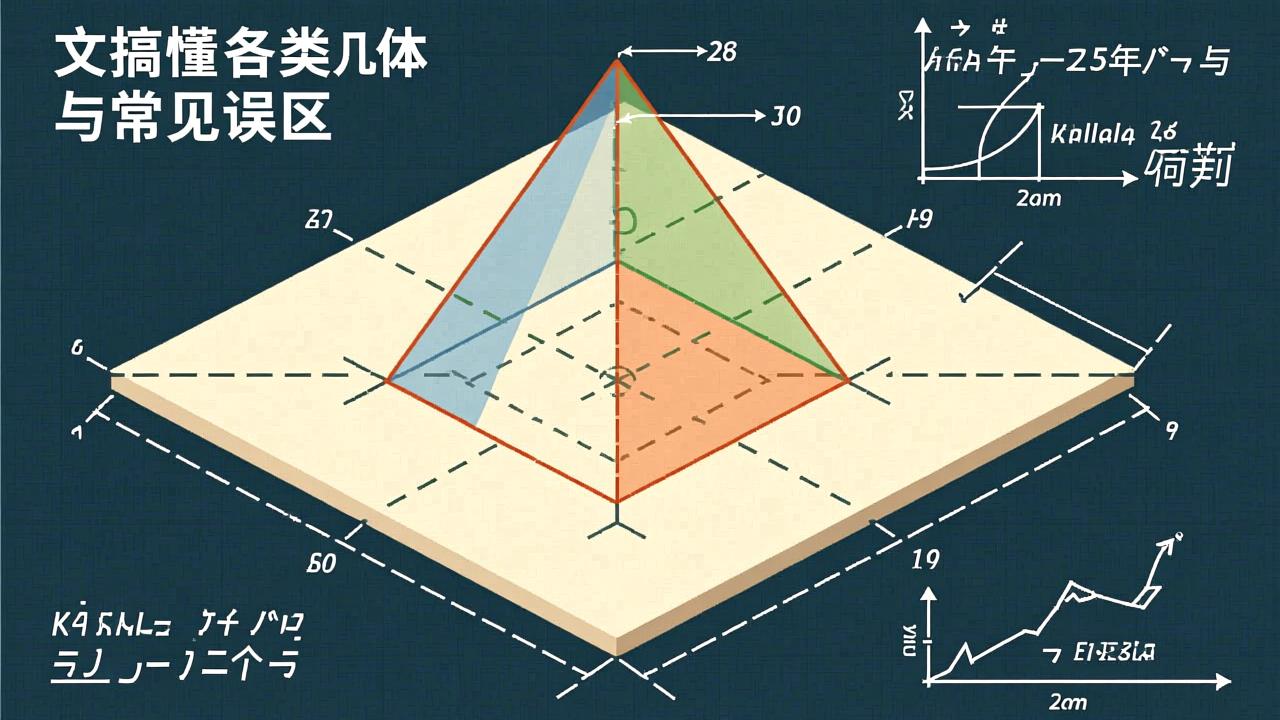
说到圆柱，我脑子里第一个蹦出来的就是一根水管或者一罐饮料。它的上下两个面都是圆，而且大小完全一样。所以当我们说“圆柱的底面积”，其实就是指其中一个圆形面的面积。那怎么算圆的面积呢？我记得老师当年教我们的时候用了个特别形象的说法：“π乘半径平方，就像把圆切成无数小扇形再拼成一个近似长方形。”

公式很简单：底面积 = πr²。这里 r 是底面圆的半径，π 约等于 3.14。这个公式其实是有推导过程的，但对我们日常使用来说，记住它就够了。比如一个饮料罐的底面半径是 4 厘米，那它的底面积就是 3.14 × 4² = 50.24 平方厘米。这个数字虽然不大，但它可是计算整个罐子能装多少液体的关键一步。

有一次我去超市买油漆，看到桶身上写着直径 30 厘米，我就顺手算了下底面积。半径是 15 厘米，代入公式就是 3.14 × 15² ≈ 706.5 平方厘米。虽然这只是个估算，但让我大概知道这桶油漆底部有多大，搬运时也更有数了。所以说，别小看这个公式，生活中真能用上。

2.2 长方体底面积计算公式：长×宽的应用场景

长方体是我们最熟悉的立体图形之一，像书本、鞋盒、冰箱，几乎无处不在。它的底面是一个长方形，所以底面积的计算方式就是小学就学过的“长乘以宽”。公式写出来就是：底面积 = 长 × 宽。

我一直觉得这个公式太简单，反而容易被人忽略它的意义。其实关键在于——你得先判断哪一面是“底”。比如一个扁平的纸箱，如果平着放，底面可能是那个大的长方形；但如果竖起来放，底面就变成了一个小的侧面。数学上我们通常按图形结构来定底面，而不是看怎么摆放。一般选那对平行且相等的面作为上下底，这样方便统一计算体积。

有次我家装修，工人要铺地砖，我拿着房间尺寸图一看，长 6 米，宽 4 米，瞬间反应过来：这不就是一个大长方体的底面吗？底面积就是 6×4=24 平方米。这个数据直接决定了要用多少材料。你看，哪怕是在装修现场，底面积的概念也在悄悄起作用。只要搞清楚哪个面是底，计算就变得非常直观。

2.3 正方体、棱柱与圆锥等其他立体图形的底面积计算方法

正方体其实是长方体的一种特殊情况，六个面都一样大，每个面都是正方形。所以它的底面积就是边长的平方，也就是 边长 × 边长 或者写作 a²。比如一个魔方，边长 5 厘米，底面积就是 25 平方厘米。因为所有面都相同，无论你怎么放，随便挑一个当底都没问题。

再来说棱柱。棱柱的种类比较多，有三棱柱、四棱柱、五棱柱等等，区别就在于底面是三角形、四边形还是五边形。但规律很明确：底面积就是那个多边形的面积。比如三棱柱的底面是个三角形，那就用三角形面积公式（底×高÷2）去算；如果是正六棱柱，底面是正六边形，可能需要拆成六个等边三角形来计算。我做题时喜欢先把底面单独画出来，当成一个平面题来做，思路立马清晰很多。

最后说说圆锥。它只有一个底面，是个圆形，另一个端点是尖尖的顶点。所以它的底面积和圆柱一样，也是 πr²。很多人会误以为圆锥有两个底，其实不是。正因为只有一个底面，在计算体积时公式变成了“底面积×高÷3”，比圆柱少了个三分之二。这点特别容易混淆，我以前考试就栽过跟头。

这些图形看起来五花八门，但只要你抓住一个核心：先识别底面形状，再套对应的平面面积公式，底面积怎么求的问题基本都能解决。不管是规则的还是稍复杂的，方法都是相通的。

在学习了几何体底面积的基本计算方法后，你会发现课本上的题目大多很规整——圆柱就是标准的圆形底面，长方体也是四四方方的。但现实世界可没那么“听话”。很多时候我们面对的是不规则形状、摆放方式奇怪的物体，甚至单位还不统一。这时候光会套公式就不够了，得掌握一些实用技巧。我来分享几个我在实际生活中总结出来的经验。

3.1 如何识别复杂图形的底面

刚开始学立体几何时，我也总搞不清哪个面才是“底”。老师说“底面是支撑物体的那个面”，听起来挺合理，但在数学题里并不完全适用。比如一个斜放的三棱柱，它靠一个侧面立着，那这个侧面是不是底呢？其实不是。在几何计算中，“底面”通常是成对出现的两个平行且全等的面之一，而不是物理上接触地面的那个面。

举个例子，有一次我在帮朋友设计一个小木屋模型，屋顶部分是个斜顶结构，看起来像一个倾斜放置的三棱柱。他问我体积怎么算，我就先让他找出哪两个面是相同的三角形，并且互相平行。这两个三角形才是真正的“底面”。一旦确定下来，底面积就能用三角形面积公式算出来，再乘以高就得到了体积。所以说，在面对复杂图形时，不要被它的摆放姿势迷惑，关键看是否有两组对称、平行又相等的面。

还有些组合体更麻烦，比如一个圆柱上面摞了个长方体。这种情况下没有统一的底面，我们需要分块处理。通常以最下面那个图形的底面作为整体的参考底面。如果是求整个物体占地面积，那就只看最底部接触地面的部分；但如果要算总体积，就得分别求出每个部分的底面积和高，再逐个计算后加起来。这种拆解思维特别重要，把大问题切成小块，每一块都变得容易解决。

3.2 单位换算对底面积计算的影响

很多人算错底面积，不是因为不会公式，而是栽在了单位上。你有没有试过用米和厘米混着算？结果数字差了一大截，自己还莫名其妙。我记得有次给阳台做防水，测量数据是长3.6米，宽400厘米。我当时直接拿3.6×400=1440，以为面积是1440平方米，吓了一跳——这比我家还大！后来才反应过来，单位不一致，不能直接乘。

正确的做法是先把所有长度单位统一。400厘米等于4米，所以底面积应该是3.6×4=14.4平方米。你看，差了一个数量级。底面积的单位是平方单位，所以单位换算时要格外小心。比如从厘米换到米，数值除以100，但面积要除以10000（因为1平方米=10000平方厘米）。很多人忘了这一点，导致最终结果偏差巨大。

再举个装修的例子。我去买地毯，店员报的尺寸是“250厘米×300厘米”，而商家标价按“平方米”收费。如果我不换算，直接当成2.5×3=7.5元就完事了，那就亏大发了。实际上面积是2.5×3=7.5平方米，再乘单价才是总价。所以每次动手算之前，我都会提醒自己一句话：“单位齐了吗？”只要单位对齐了，后面的计算基本就不会出岔子。

3.3 结合实际问题进行底面积求解

理论归理论，真正让我理解底面积意义的，还是在生活中一次次的实际应用。比如家里要买鱼缸，我想知道能装多少水，就必须先算底面积。一个长80厘米、宽40厘米的矩形鱼缸，底面积就是80×40=3200平方厘米，也就是0.32平方米。再乘以水深（假设50厘米），就能得出体积大约是160升。这样我就能判断是否适合养某种鱼类，避免买回来才发现太小。

另一个常见场景是建筑基础施工。去年我家翻修院子，工人打地基前要算混凝土用量。地基横截面是个梯形，长条状延伸。他们告诉我，这种属于棱柱类结构，底面就是那个梯形。于是我就用梯形面积公式（上底+下底）×高÷2 来算底面积，再乘以长度得到总体积。虽然这不是标准的长方体或圆柱，但原理一样：找底面、算面积、乘高。

还有一次参加社区绿化项目，我们要铺草坪。地面是一块不规则四边形，没法直接套公式。我们的办法是把它分割成两个三角形，分别测量边长和高，算出每个三角形的面积后再相加。这种方法叫“分割法”，在处理非标准图形时非常管用。只要你能把复杂图形拆成几个熟悉的平面图形，底面积的问题也就迎刃而解了。

这些经历让我明白，底面积不是一个死板的数学概念，它是连接抽象公式和真实世界的桥梁。无论是装水、建房还是种草，只要涉及到“占多大地方”或者“能装多少东西”，背后都有底面积的身影。学会灵活识别底面、注意单位统一、结合具体情境分析，才是真正掌握了“底面积怎么求”的精髓。

学了这么久的底面积计算，我回头看看自己刚开始的样子，真是错得五花八门。那时候总觉得会背公式就万事大吉，结果一做题就出错，考试更是频频丢分。后来我才明白，很多同学和我一样，不是不努力，而是掉进了几个常见的思维陷阱里。现在我把这些坑一个个挖出来，再告诉你怎么绕过去，希望能帮你少走点弯路。

4.1 学生在“底面积怎么求”中常犯的错误

最典型的错误就是乱套公式。比如看到一个立体图形，不管三七二十一，直接拿长乘宽去算底面积。可问题是，那个图形根本就不是长方体！有一次我在辅导表弟数学时，他遇到一个圆锥体积题，题目让他先求底面积。他二话不说写了“长×宽”，我问他：“圆锥的底面是啥形状？”他愣了一下才反应过来——是圆形啊！这说明他对“不同图形对应不同面积公式”这个基本概念都没建立起来。

另一个常见问题是搞不清“底面”到底是谁。有些学生以为物体放在桌面上的那个面就是底面，其实不然。几何中的“底面”更多是从结构角度定义的，通常是成对出现、平行且全等的两个面之一。比如一个横着放的圆柱，虽然它是侧着躺的，但底面依然是两头的圆。我以前也纠结过这个问题，直到老师画了个斜切的圆柱模型，指着两端说：“无论你怎么摆，这两个圆始终是对称的，它们才是底。”这句话让我一下子通了。

还有人容易忽略单位问题。前面讲过单位不统一会导致结果差十万八千里，但很多人还是记不住。特别是当题目给的数据一会儿是厘米，一会儿是米，甚至还有毫米混进来的时候，他们常常忘记换算，直接代入计算。最后答案看着像模像样，其实早就错了。我自己吃过亏之后，现在每次做题第一件事就是检查所有长度单位是否一致，养成习惯后几乎不再出错。

更隐蔽的一个误区是混淆“底面积”和“表面积”。有次模拟考，题目问的是“这个盒子底部占多大面积”，明明是在问底面积，可班上有不少人把六个面加起来算了。这说明他们对“底面积”的实际意义理解不够深。其实只要想想生活中“占地面积”这个词，就知道它只关心接触地面的那一面，而不是整个外壳。

4.2 提高空间想象能力的方法

说实话，刚学立体几何时，我对图形的空间关系特别模糊。脑子里想的是平面图，眼睛看的是立体题，中间缺了一环。后来我发现，提升空间感并不靠死记硬背，而是要动起来——用手、用眼、用身体去感受。

我开始随身带一套简易几何模型，就是那种塑料拼插的小立方体、圆柱、棱锥。没事就拿出来摆一摆，转一转。比如把一个三棱柱翻来覆去地看，观察哪两个面是相同的三角形，试着从不同角度画出它的投影。慢慢地，我就能在脑海里“旋转”这个图形了。现在哪怕题目只给一个文字描述，我也能迅速在心里构建出它的样子。

还有一个特别有效的方法是画草图。别小看这一步，很多学生嫌麻烦，直接心算，结果方向一错全盘皆输。我的做法是：读完题立刻动手画个简图，标出已知条件，用箭头指明哪个是高，哪个是底面。哪怕画得歪歪扭扭也没关系，关键是让抽象的文字变成可视的图像。有一次做一道斜放棱台的题，全班只有几个人做对，而我是靠着画图一步步推出来的。

我还喜欢用生活物品辅助理解。比如拿个水杯当圆柱，书本当长方体，饭盒当棱台。把这些东西拿在手里转一圈，问问自己：“如果我要算它的体积，该选哪个面作底？”这种具象化的练习比刷十道题都管用。空间想象力不是天生的，它是通过一次次“看见”和“触摸”培养出来的。

4.3 推荐练习题型与教学资源

要想真正掌握“底面积怎么求”，光听懂课不行，必须大量练习有针对性的题目。我自己总结了几类特别值得反复做的题型。第一类是“识别底面”的判断题，比如给出几个不同摆放方式的立体图，让你选出正确的底面并说明理由。这类题不考计算，专治概念模糊。

第二类是单位混合作业题。比如题目给的数据分别是分米、厘米、米，要求你先统一单位再计算底面积。这种题练多了，你会自然而然形成“单位敏感度”，一看数字就知道要不要换算。我还建议自己出题来练，随便编一组数据，故意掺进不同的单位，然后挑战自己能不能一次算对。

第三类是组合图形拆分题。像L形柱体、T形基础、上下叠放的不同立体等，都需要你先分解结构，再分别找每个部分的底面。这类题最接近真实应用场景，也能锻炼逻辑思维。我曾经在一个学习网站上找到一套动态拆解动画题，鼠标一点就能看到图形如何被切成几个规则部分，直观又有趣。

说到资源，推荐几个我觉得特别实用的。B站上有位数学老师讲《立体几何入门》系列，语言通俗，配合手绘动画，非常适合初学者补基础。另外“洋葱学院”APP里的互动练习很贴心，每步操作都有反馈，错了还会提示哪里出了问题。如果你喜欢纸质资料，《初中数学典型题精讲》这本书里的几何章节编排得很系统，从识图到计算层层递进。

最后我想说，别怕犯错。我在学这部分内容时错过的次数数都数不清，但每一次错误都在帮我建立更清晰的认知。只要你愿意停下来反思“为什么错”，并且主动去弥补漏洞，底面积这个问题迟早会被你彻底拿下。